原点 O,単位点 E の数直線 OX 上に,座標が a の点 A が与えられたとき,座標 √a の点 P を作図します。 をクリックすると途中経過が示されます。のような正の数の平方根の必要性と意味を理解し,正の数の平方根を含む簡単な式の計算ができるよ うにするとともに,具体的な場面で平方根を表したり処理したりすることができるようにすることが ねらいである。 (2)指導観 javalangMathsqrt (double a) 返回正确舍入的一个double值的正平方根。 特殊情况: 如果参数是NaN或小于为零,那么结果是NaN 如果参数是正无穷大,那么结果为正无穷大 如果参数是正零或负零,那么结果是一样的参数 否则,其结果是最接近真正的数学平方根的
Q Tbn And9gctisfnlhcrvkbipgi7gyhzqghnfkjyqzlwt Ghvae2zsnt Fatb Usqp Cau
正の平方根 求め方
正の平方根 求め方-Start studying 数A 用語 Learn vocabulary, terms, and more with flashcards, games, and other study tools平方根 2 単元について (1)単元観 本単元は,学習指導要領の内容の〈A数と式〉「(1)正の数の平方根について理解し,それを用 いて表現し考察することができるようにする。」に基づいて設定したものであり,その内容は以下 の3点である。



Sqrt
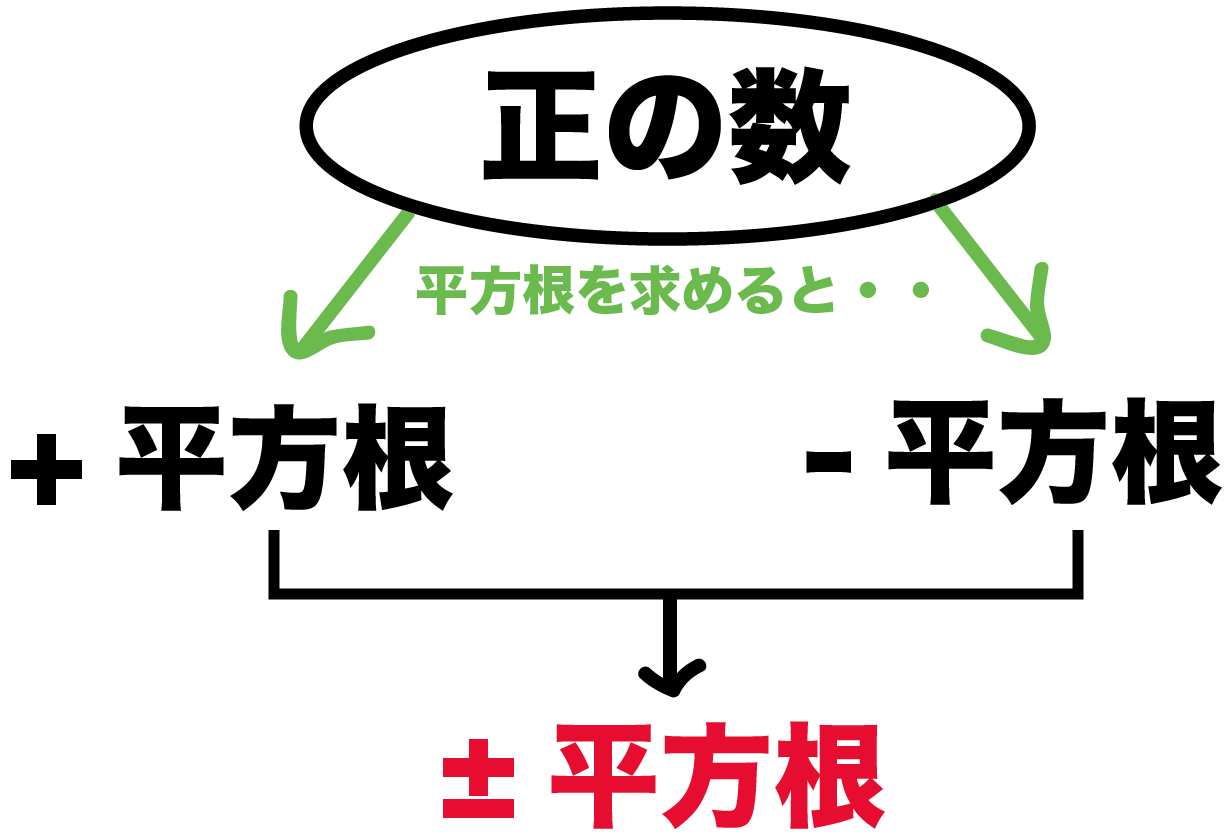
平方根関数 入力 x に対してその非負の平方根 x {\displaystyle {\sqrt {x}}} 正の平方根函数のグラフ。 これは放物線の半分になっている。 正の平方根函数 √ は 連続 かつ x > 0 で 微分可能 であり、 導関数 は d d x x = 1 2 x {\displaystyle {\frac {d} {dx}} {\sqrt {x}}= {\frac 平方根とは2乗してその数になるものをいうので 25の平方根は±5、 6の平方根は±√6 です。 計算するときは √6は正の数、-√6は負の数として計算します。のように整数にならないような場合も表せます。負の数の平方根は存在しないので根号 \(\sqrt{}\) の中は必ず正の数になるので、 「\(x\) の平方根」 が \(±\sqrt{x}\) であるとき \(x\) の値は必ず正の数にな
つまり1の平方根は±1 (□) 2 = 9のとき □には3, または3がはいるので、9の平方根は±3 このように 正の数の平方根は、正と負の2つあり、それらの絶対値は等しい。 秘書ザピエル今回は、「平方根(へいほうこん)」についての内容です第4回として、「平方根の求め方 分数 小数 実践編」について、解説してもらいたいと思います。では先生、お願いします!数学おじさんX 的平方根是 平方为 x 的数 : r2 = x
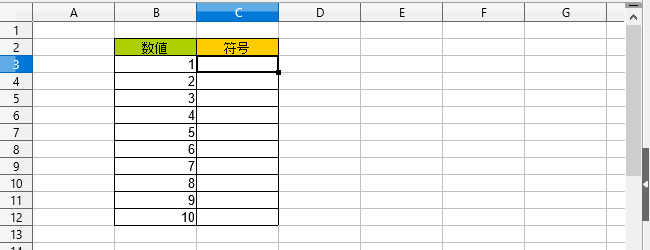
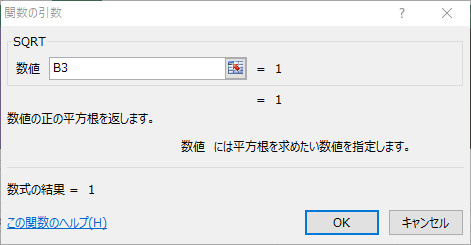
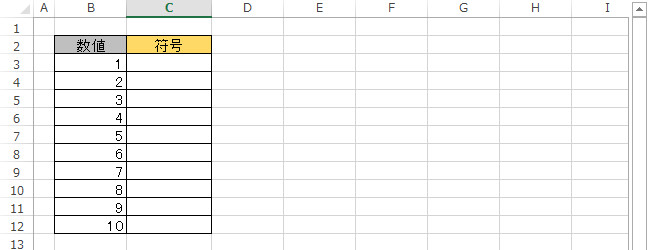
数値の正の平方根を返します SQRT(値) 値:平方根を求める星の数値。 問題 サンプルファイル GoogleDreiveで表示されます。ダウンロードし、Excelで開いてください。 各数値の、正の平方根を求める。 回答 セル「C3」を選択状態にする。 正方形の1辺の長さは、面積の平方根によって求めることができるので 0の正の平方根が1辺の長さとなります。 $$0の正の平方根=\sqrt{0}=10\sqrt{2}cm$$ よって、1辺の長さは\(10\sqrt{2}\)㎝が答えとなります。 平方根の利用まとめ!している。そこで,本単元では2 乗してa(a≧0)になる数の必要性から平方根を導入し,正の 数の平方根を含む簡単な式の計算ができるようにするとともに,数の範囲を無理数にまで拡張す る。こうして数の概念についての理解をより深めていくことになる。



平方根の定義と基本的な公式 思考力を鍛える数学




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ
一个正数有两个实平方根,它们 互为相反数 , 负数 没有平方根,0的平方根是0。1 つの正の数に対して、その平方根は正と負の 2 つあり、そのうち正の方を √a a と書き、ルート a と読みます。 このページでは、平方根(ルート)の 意味 と 計算方法 、 性質 、そして 大小関係 について説明しています。このような正の数の平方根の必要性と意味を理解し、正の数の平方 根を含む簡単な式の計算ができるようにする。 具体的な場面として、高知県数学思考力問題集「紙の規格を調べよう(3-2-B)」を活用し、B4 判の紙はB5 判の紙と比




数と式 平方根について 日々是鍛錬 ひびこれたんれん




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ
・正の数の平方根を,根号を使って表すこ とができる ・根号の意味を理解している。 2 平方根の大小(1) いろいろな数の平方根を 数直線上に表すことで, 大小関係を理解し,不等 号を用いて表す。 平方根を計算するにはsqrtメソッドを使います。平方根を求めたい値を引数として指定し、戻り値はdouble型で返却されます。 PR Javaプログラミングで挫折しない学習方法を動画で公開中 実際に書いてみよう 整数4の平方根を求めるサンプルです。 よって、平方根を求めようとする数値から平方根の値を持つ整数の個数の値、3,5,7,9,・・・を順番に引いていき、0以下になった回数が求める平方根の値となります。 具体的な数値で確かめてみましょう。例えば19の場合、1回目の計算 193=16、2回目の計算 165=9、3回目の計算 97=2、4回目の計算 29



初中数学求算术平方根 有人秒出答案 有人无从下手 原因在这儿




平方根とは コトバンク
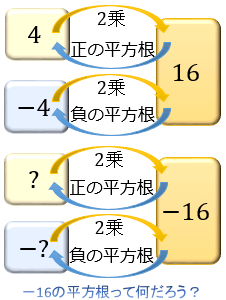
平方根とは 平方根とはなんでしょう? 例えば3や3を2乗すると9になります。 このときの3や3を9の平方根といいます。 つまり2乗するとある数になる数を平方根というってことです。 そんなに難しくなさそうですね。 それでは例題をしてみましょう正の平方 根の意味と必要性を理解するために,できるだけ身近な事象と関連付けて理解できるようにし ていく。具体的には, 2乗するとaになる数を考察するために正万形を用いて,正方形の面積 とその1辺の長さの関係から考えさせていきたい。また,大小数 a が与えられたとき、二乗(平方)して a となる数、つまり、 x2 = a となる数 x を a の平方根という。 a が正の数のときは、 a の平方根は正の数、負の数それぞれ一つずつあり、その絶対値は等し




平方根とは すうがくのいえ



ワークの答えに 2aは二乗すると2aの二乗になるから 2aの二乗の正の平方根 Yahoo 知恵袋
的算术平方根记为,读作"根号a",a叫做被开方数。 ③规定:0的平方根是0。 ④负数在实数范围内不能开平方,只有在复数范围内,才可以开平方根。 例如:1的平方根为±1,9的平方根为±3。 ⑤平方根包含了算术平方根,算术平方根是平方根中的一种。 したがって、36の平方根は6と6の2つがある のです。(それぞれ正の平方根、負の平方根と言います) つまり、 ある数の平方根はプラスとマイナスの2種類ある ということを覚えておきましょう! テストでは正と負、両方書かないとバツになりますよ! 平方根の定義 a a を実数とします. 2 2 乗すると a a になる数のことを a a の 平方根 と言います.言い換えると, a a の平方根とは, 2 2 次方程式 x2 = a x 2 = a の解のことです. 正の実数 a a の平方根は必ず 2 2 つあり,それらは絶対値が等しく,符号が異なり



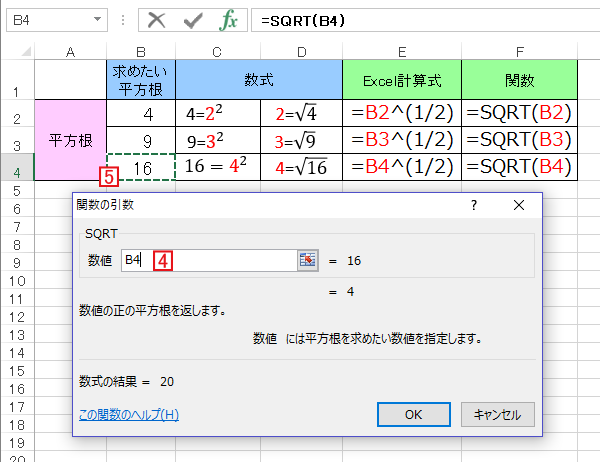
Excel関数 平方根 ルート を求める Sqrt関数




センター数 A 追第1問 大学受験in北海道
平方根の表し方を考えよう。 正の数a の平方根には,正の数と負の数の2つがある。 これらの平方根を,記号 を使って次のように表す。 正のほうを a,負のほうを- 0の平方根は0だから, 0=0である。 を使って平方根を表す




平方根 Wikipedia
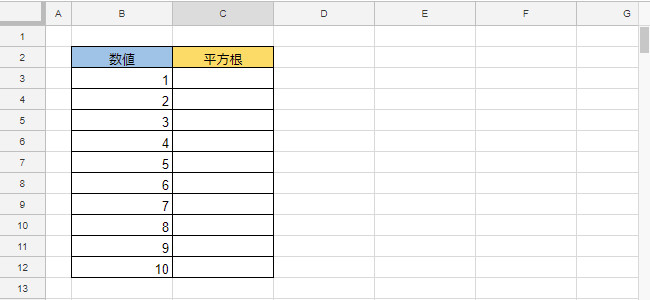



Sqrt 正の平方根を求める スプレッドシート関数




3の平方根 Wikipedia




Petrificater 木宮ぴあ はいそうですー ただ 計算上の 4は正の平方根として計算するので 2 2ですねー 2 2とは表しませんー




数と式 平方根について 日々是鍛錬 ひびこれたんれん



1



1



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




中3数学 平方根の計算の仕方を極めよう 掛け算 割り算も 都立高校受験応援ブログ




田村 良輔 あぶない計算 平方根 正の平方根 ルート 根号 ルート4 2 ルート9 3 ルート25 5 Kyon2 キョンキョン 小泉今日子 キョン は シカ科 しゃぶしゃぶ 麻薬




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




正の平方根ってなんですか 笑 よく分からないです 教えてくれる方いたら嬉しいです Clear
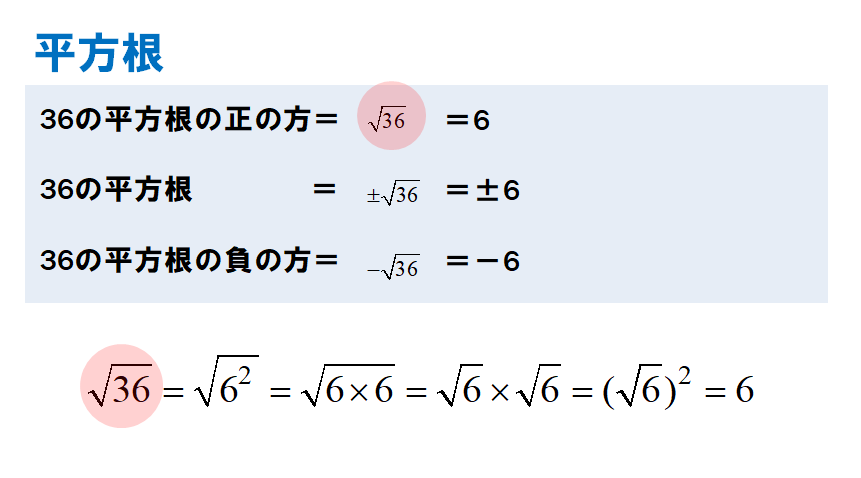



中3数学 平方根の性質の定期テスト対策問題 Examee



2乗 平方根




答えは 1 121 2 A二乗の正の平方根がaとなるから 3 5 Clear




4の平方根やルートは 9 16 25 36 49の平方根とルートは 平方根とルートの違い 意味 や計算方法を解説 プラスマイナス More E Life



6 なぜ は正の方だけ表すのか 数学史による考察 アクチュアリー試験数学の研究




数と式 平方根について 日々是鍛錬 ひびこれたんれん



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




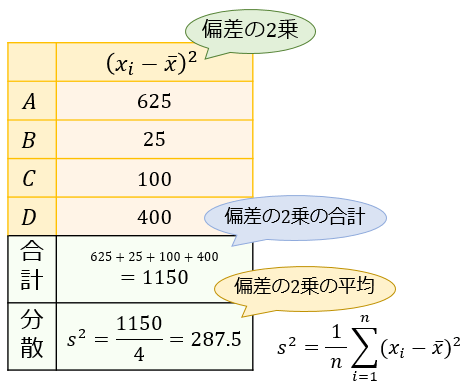
教師の統計学 標準偏差を求める意味は なぜ分散の正の平方根なのか 高校教師とictのブログ 数学 情報 Ict



平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




平方根についての雑感 中学3年の数学 身勝手な主張
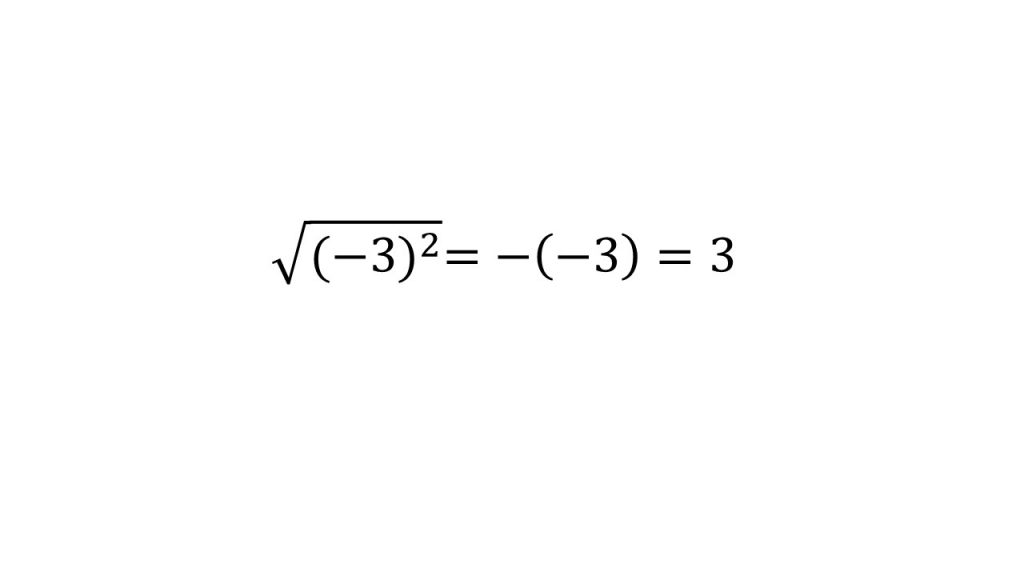



根号 ルート の中に2乗があるときの対処法 根号 ルート は 正の平方根 という意味です 大学受験の王道



Sqrt 正の平方根を求める Calc関数




数と式 平方根について 日々是鍛錬 ひびこれたんれん



Sqrt 正の平方根を求める Excel関数




正の数や負の数の乗法や除法 割り算が出たら掛け算に戻す習慣を 中学や高校の数学の計算問題



1



電卓でルート 平方根 を計算する方法




複素数の平方根1 定義と高校数学の両面から考える 身勝手な主張



Q Tbn And9gctisfnlhcrvkbipgi7gyhzqghnfkjyqzlwt Ghvae2zsnt Fatb Usqp Cau



Sqrt



中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく




平方根についての雑感 中学3年の数学 身勝手な主張



数学の質問です 分散の正の平方根が標準偏差ということまではわかるので Yahoo 知恵袋



Sqrt 正の平方根を求める Excel関数




この公式の証明がしたいのですが わからないので教えてほしいです Clear




中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく




平方根 2乗するとaになる数 教遊者



べき乗 Nのm乗 平方根 ルート 立方根を利用 Excel エクセル の使い方




2 つの図の正の平方根 アイコンのベクターアート素材や画像を多数ご用意 Istock




この問題で 5を証明するのがわかりません Clear




中3数学 平方根 Youtube
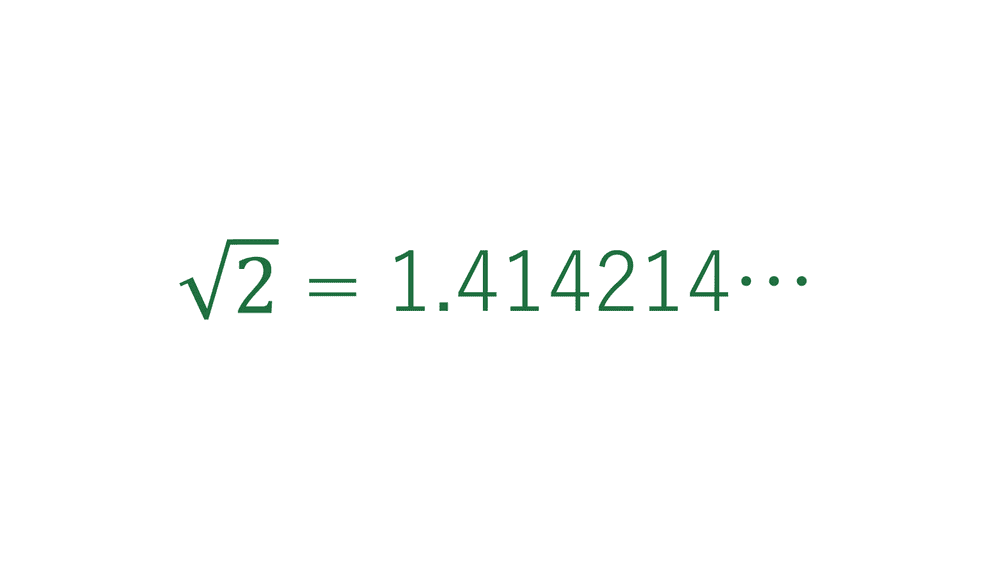



エクセルでルート 平方根 を表示 計算する方法 関数使用 Office Hack



6 2 標準偏差 統計学の時間 統計web




8 3 A Descubre Como Resolverlo En Qanda




正の平方根を求めるアルゴリズム Qiita



Http Yonominami J Saitama City Ed Jp Subj Suugaku Subj Math 3002 Pdf




正の実数に対して正の平方根はただ一つに決まる の証明 データマイナーakitoの数学館




3の平方根 Wikipedia



画像あり エクセルの関数を使ってルート 平方根 を計算 表示するには 基本と応用 ワカルニ




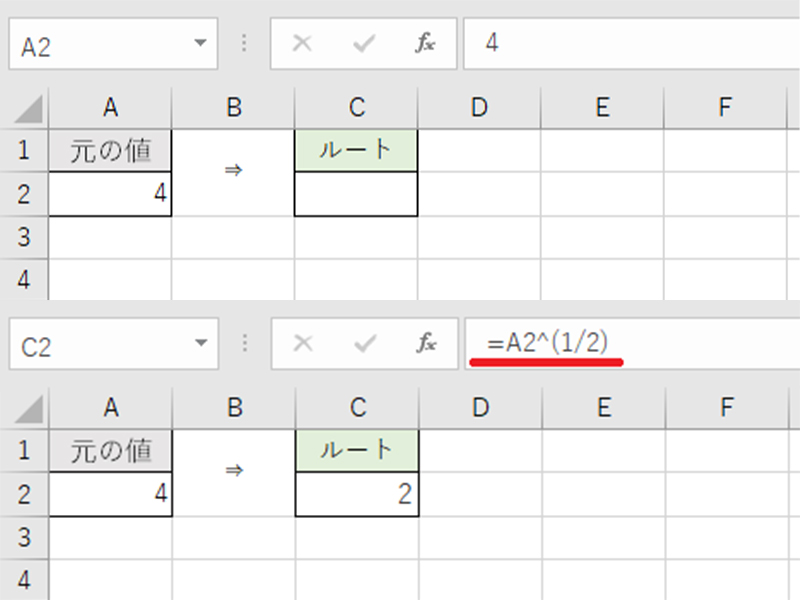
Excel エクセル で平方根 ルート を計算する方法をご紹介 Sqrt関数 Power関数 Aprico
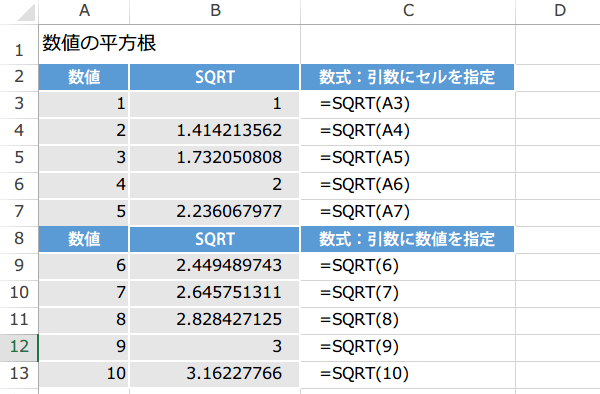



Sqrt関数の使い方 数学と三角関数関数




平方根 とは 根号の意味や性質 値の求め方について 数学fun



中学数学単元別 平方根 数学 中学校 教材 問題集 302 学林舎 通販 Yahoo ショッピング




例題 平方根與未知數 數學 均一教育平台




Sqrt関数の使い方 数学と三角関数関数




Excel Sqrt関数 正の平方根 ルート を求める 楽々生活 資産運用とゲームで稼ぐブログ



標準偏差とは何か その求め方や公式の意味 使い方をわかりやすく説明します アタリマエ




3の平方根 Wikipedia




5の平方根 Owlapps
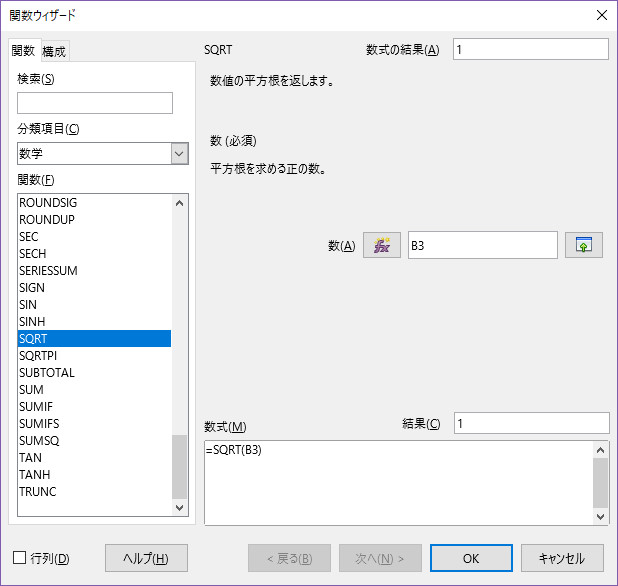



Sqrt 正の平方根を求める Calc関数



へいほう こん 平方根 ヘイハウ 広辞苑無料検索 大辞泉



平方根の問題なのですが13の正の平方根の答えは 13だと思っているのですが Yahoo 知恵袋
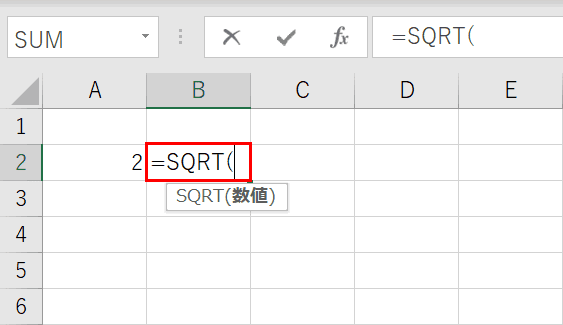



エクセルでルート 平方根 を表示 計算する方法 関数使用 Office Hack




Sqrt関数の使い方 数学と三角関数関数




数と式 二重根号について 日々是鍛錬 ひびこれたんれん




2r Descriptive Statistics By R 8r Numeric Data




平方根とは コトバンク



平方根って9の平方根だと3と 3の2つですが 9だと 3だけで Yahoo 知恵袋




2の平方根 Wikipedia




中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく
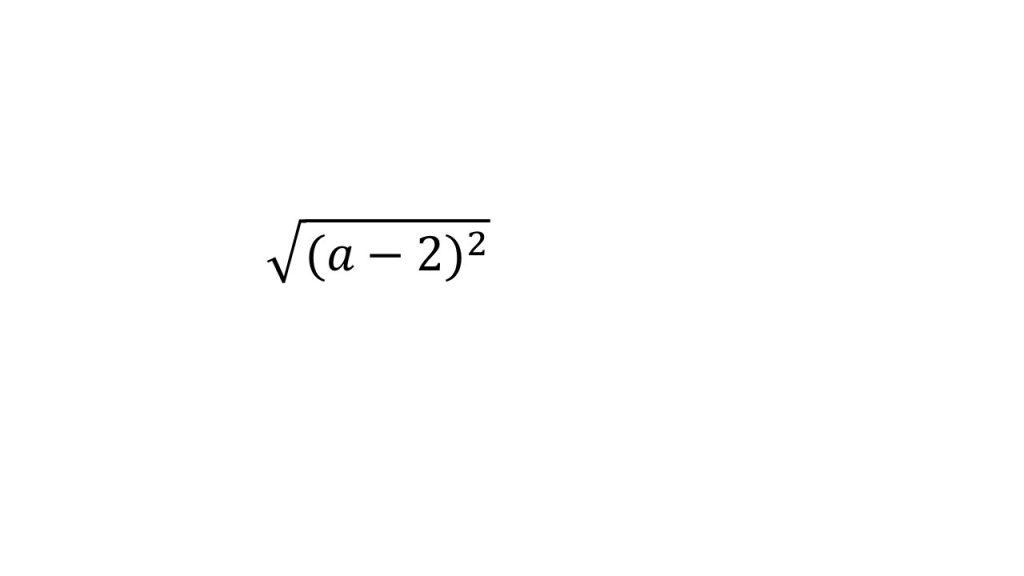



根号 ルート の中に2乗があるときの対処法 根号 ルート は 正の平方根 という意味です 大学受験の王道




この問題の解説をお願いします Clear




Bartarc 3 Lihat Cara Penyelesaian Di Qanda



Http Www Naka H Ibk Ed Jp Action Common Download Main Upload Id 2375




平方根の利用 1 整数 自然数になるようなn 標 難 数学の解説と練習問題




標準偏差とは何か その求め方や公式の意味 使い方をわかりやすく説明します アタリマエ




正平方根 Youtube
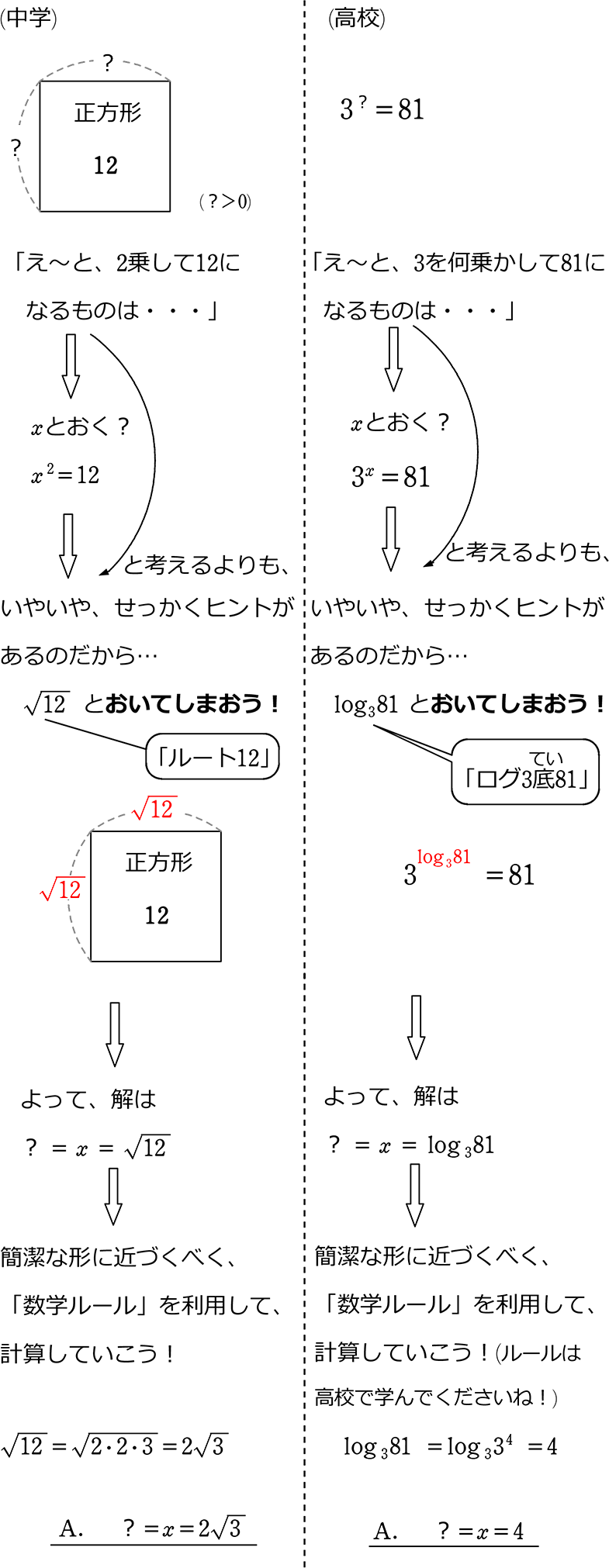



中学数学 平方根



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




例題 求正負平方根 1 Youtube
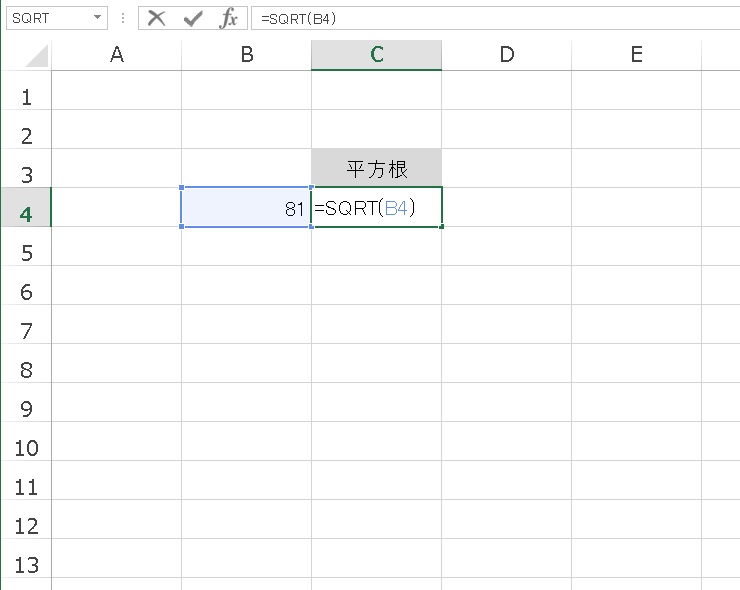



エクセルで平方根 ルート を求めるsqrt 関数 統計学が わかった




2 つの図の正の平方根 アイコンのベクターアート素材や画像を多数ご用意 Istock




数学i 数学i39 12ギョウザで分散偏差の2乗の平均値標準偏差分散の正の平方根 Youtube



Sqrt関数 正の平方根を求める Perl入門ゼミ



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




平面図形37 平方根の作図 怜悧玲瓏 高校数学を天空から俯瞰する




宇宙を歩く高校数学 基礎




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月




Rrigad 5 3 Descubre Como Resolverlo En Qanda




平方根 ルート64 8 ではない の意味がわかりません 中学数学 定期テスト対策サイト
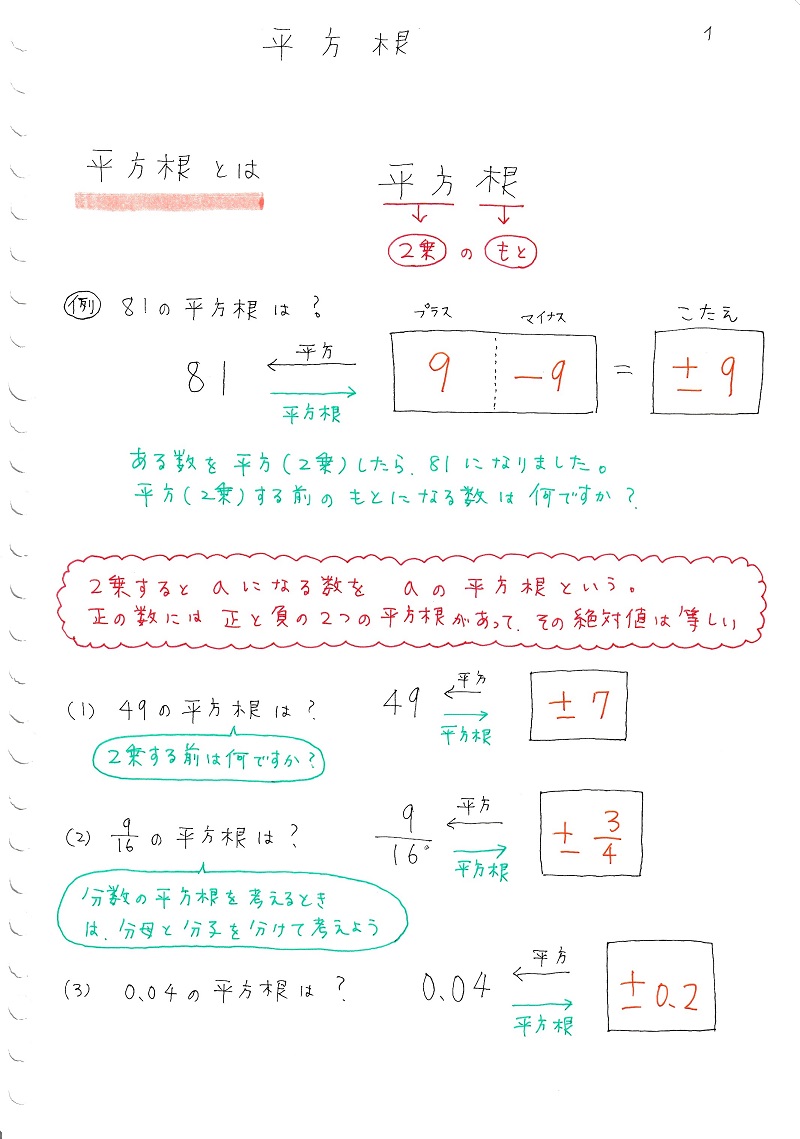



中学数学 平方根 ママ塾ノート


